Funny Way to Multiply Two Numbers With The Same Tens Digit
I may have peaked in second grade
Written by latentCall145 on September 7, 2024 (changelog)
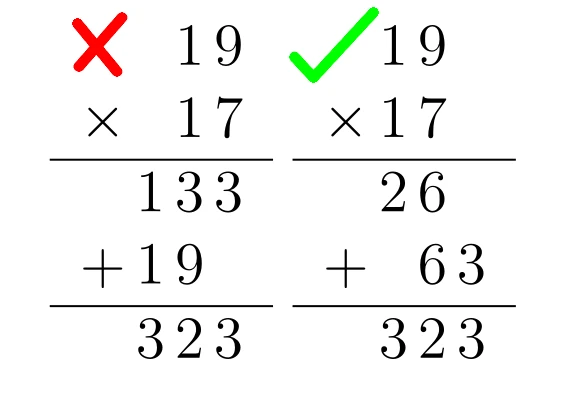
Two methods. Same result under certain conditions. The right method is easier.
Context
I'm in second grade and in math class. The unit? Multiplication. Easy, I think to myself. My grandparents forced me to memorize my times tables last summer instead of letting me play Roblox. I can't lie, memorizing those times tables was a struggle, but I eventually succeeded.
Even better, today we got to play a game to practice our times tables that my teacher called "Around the World". This was a king-of-the-hill type game where two students were given a problem and the first person to say the correct answer moved on to the next student. Today, I was dominating everyone at Around the World, blurting out the answers of problems left and right.
4 times 8? 32.
9 times 3? 27.
6 times 3? 18.
But for every classmate which I beat, I got one person closer to reaching A, my boogeyman (side note: A was and still is my friend. A, if you're reading this right now, hi :) ). He was the only one in the class who could answer these questions faster than me. As I closed on him, my palms got sweaty and the care-free expression on my face evaporated. If I focus, there's a chance I can win, I reassure myself. Then the time came where we were side-to-side. I was dead silent, ready to pounce.
19 times 17?
The class bursts out laughing. Everyone knew we memorized our times tables, especially the teacher, so she always gave us the crazy questions. Meanwhile, my mind is scrambling to solve the problem.
Me: 9 times 7 is 63. 1 times 7 is 7, carry 6 is 133. 1 times 19 is 19 -
A: 323.
Correct!
A usually beat me at Around the World. But I was always competitive. So, determined to beat him, I looked for tricks to quickly multiply larger numbers. After much perseverance and fiddling with numbers, I found the biggest math contribution I'll ever make to society.
The Method
1. Take two numbers, say 19 and 17. Add the top number with the ones digit of the bottom number (so 19 + 7 = 26).
2. Multiply the result from Step 1 by 10 (26 * 10 = 260).
3. Multiply the ones digits of both numbers (9 * 7 = 63).
4. Add the results from Step 2 and 3. That's your answer (260 + 63 = 323).
When I found out this formula, I was ecstatic. After some trial and error, I found it to work if both numbers were between 10 and 19 inclusive. That's a good start for Around the World purposes, but what if the teacher asks what 25 * 21 is? So I did some more searching and I eventually found that the formula worked if both numbers were between 20 and 29 inclusive as long as you multiply Step 1 by 20 instead of 10 for Step 2. From hindsight, modifying the above formula to work for numbers between 30 and 39 inclusive would be pretty easy (replace 20 with 30), but I was in second grade so I couldn't figure it out. Besides, there was no way the teacher was going to make second graders multiply numbers higher than 30. So I stopped at 20 and felt extra confident for our next round of Around the World.
But time passed.
And yet more time passed.
We never played Around the World again. Or at least I don't recall myself getting a chance to use this formula for the game.
But it wasn't all bad. Over the years, I forgot the 20-29 version of this formula, but not the original 10-19 version, which happened to be much more useful anyway. I always got a little chuckle when I encountered a multiplication of two numbers between 10 and 19, knowing that second-grade me somehow found the weirdest way to get the answer. To this day, it's still my preferred way of multiplying two numbers between 10 and 19.
The Revival
Cut to my first year of college. I was bored in class one day but I randomly remembered about my formula and wanted to find out why it worked. I knew it had to do with the distributive formula since my formula only worked if the tens digit for both numbers were the same. So I quickly found this proof:
Suppose we have numbers x, y which both have the same tens digit and are both less than 100. x, y can then be rewritten as 10n + a and 10n + b respectively where a, b, n are between 0 and 9 inclusive. Then, xy is equal to:
(10n + a) * (10n + b) =
100n^2 + 10an + 10bn + ab =
10n(10n + a + b) + ab =
10n(x + b) + ab
This is the same exact formula I found out in second grade, but since we're using algebra, we can see how general this formula is. The reason I forgot about the 20-29 version of this formula was because I didn't have the math knowledge at the time to see the connection between the 10-19 case and the 20-29 case. But we can see now that the two cases are part of the same formula. In fact, n doesn't even have to be between 0 and 9.
Conclusion
There's no moral to this story. But not all stories need morals. This was just a fun memory that I thought would be interesting to share.
Changelog
- September 7, 2024: Published this to my site